Time dilation in horizontal light clock?

No time dilation is observed in a horizontal light clock if the horizontal velocity of a pulse is considered, which was ignored in the calculation? It ticks at the same rate no matter how fast it moves.

When a pulse moves toward the rear mirror:

Although a pulse moves towards the rear mirror with “c” but it has horizontal velocity ”v” in opposite direction to “c” as well, as the moving spaceship does in which the clock consists relative to the stationary observer. Considering alone c-v means both the pulse and front/space moves in two opposite directions with “c” and "v” respectively independently. Here in this case a pulse has "c" only. It doesn't have horizontal velocity "v" (opposite to "c") as a moving clock does.

A pulse has two velocities

1- "c" towards the rear mirror and

2- "v" with which it moves forward.

The net velocity of a pulse = c-v. This is relative to a stationary observer

Physics laws are the same in all inertial frames of reference therefore a pulse must have a horizontal velocity "v" at which the horizontal clock moves when a pulse bounces toward the rear mirror.

Both a pulse and the rear mirror move with the same horizontal velocity therefore the forward velocity "v" of the rear mirror never helps a pulse to strike with it earlier as taught. So it means the striking time of a pulse (with rear mirror) increases when the horizontal velocity of the moving spaceship increases.

Time dilation may be observed in the vertical light clock used by Einstein because the horizontal velocity of a light clock added to “c” never compensated.

Addendum: If C+V is possible then aforementioned explanation is also possible.

It appears your mistake is in calculating the velocity of the pulse.
As it is a pulse of light, there is no need to calculate the velocity. It is c in all inertial reference frames.


First, lets consider it without length contraction.
The path is of length L, which will be equal for both the observer in the frame and the observer outside the frame, so Li=Lo
The speed of light in all frames is c, and the moving frame is travelling at a velocity of v.

To the inside observer, the path length is 2Li, and thus the time taken for a cycle is ti=2Li/c.
For the outside observer, the light starts at the back and moves towards the front, taking time tf.
In this time, the system has moved forwards by tf*v, increasing the distance the light needs to travel by this amount.
So we get the following equations:
tf*c=Lo+tf*v.
tf*c - tf*v=Lo
tf*(c-v)=Lo
tf=Lo/(c-v)

For the trip back we have the back move forwards, reducing the length the light needs to travel.
So we get the following equations:
tb*c=Lo-tb*v.
tb*c + tb*v=Lo
tb*(c+v)=Lo
tb=Lo/(c+v)

So the total time to the outside observer is:
to=tf+tb
to=Lo/(c-v)+Lo/(c+v)
to=Lo*[((c+v)+(c-v))/((c-v)(c+v))]
to=Lo*[(c+v+c-v)/(c^2-v^2)]
to=2*Lo*c/(c^2-v^2)
to=(2*Lo/c)*(1/(1-v^2/c^2))
to=(2*Li/c)*(1/(1-v^2/c^2))
to=ti/(1-v^2/c^2)

So even without considering length contraction, we get time dilation in a horizontal light clock.
The reason it doesn't match is because we haven't considered length contraction.
If we do, then L for the inside frame is given by:
Lo=Li*sqrt(1-v^2/c^2)

This then modifies the 2nd last step of the above:
to=(2*Lo/c)*(1/(1-v^2/c^2))
to=(2*[Li*sqrt(1-v^2/c^2)]/c)*(1/(1-v^2/c^2))
to=(2*Li/c)*(sqrt(1-v^2/c^2)/(1-v^2/c^2))
to=ti/sqrt(1-v^2/c^2)

Which then does match that for the vertical clock.

in your case, when a pulse strikes the front mirror, it bounces back but moves forward rather than going backward forthwith as shown in the upper diagram. So how would you find the distance x which =ct2 or t2 in the lower diagram? t1 of next second starts where t2 of first / previous second ends

Detail of a start and end of each second in the horizontal light clock in your case (upper figure) and the case (lower figure) as explained above. They don't match.
Lower figure: The t1 of the first second ends at B' while its t2 at A" (from B' to A"). Next second starts at A". Is this overlap of t1 with t2 or vice versa possible?

in your case, when a pulse strikes the front mirror, it bounces back but moves forward rather than going backward

No, it starts going forward from the back mirror. It strikes the front mirror, bounces, and starts going backwards.

The fact that your first diagram has it moving forwards should be a good indicator that you are doing something wrong.

What you want is something like your second diagram, which matches what I was describing.
Here is a colour coded diagram:

Orange indicates the constant distance L.
The purple and red lines are for the forwards path.
The red line is the distance the light has travelled in this time, c*t1.
The purple line is the distance the clock has moved, v*t1.
We can see that the length of the light path is the orange line plus the purple line.
Thus c*t1=v*t1+L, thus t1=L/(c-v).

The blue and green are for the backwards trip.
The light path is blue, moving backwards, with a distance of c*t2.
The green is the clock, moving forwards, with a distance of v*t2.
We can see that now the length of the clock is equal to the light path blue the green line.
Thus L=c*t2+v*t2.

Or to express it differently, we see that the light path is the orange line minus the green line:
c*t2=L-v*t2.

Either way, you end up with t2=L/(c+v)


And there is nothing wrong with the times overlapping like that. Just consider a stationary clock, with the light bouncing back and forth, the times will always overlap.

In order to avoid that overlap, you would need to flip the entire system around at each reflection, effectively to present it from the perspective of the light.
This keeps the light always moving to the right, while the system switches between moving left and right at each reflection (and turns around so the light always moves from the left to the right).

Quote from: E E K on November 23, 2020, 04:39:50 AM

in your case, when a pulse strikes the front mirror, it bounces back but moves forward rather than going backward

No, it starts going forward from the back mirror. It strikes the front mirror, bounces, and starts going backwards.

The fact that your first diagram has it moving forwards should be a good indicator that you are doing something wrong.

What you want is something like your second diagram, which matches what I was describing.
Here is a colour coded diagram:

Orange indicates the constant distance L.
The purple and red lines are for the forwards path.
The red line is the distance the light has travelled in this time, c*t1.
The purple line is the distance the clock has moved, v*t1.
We can see that the length of the light path is the orange line plus the purple line.
Thus c*t1=v*t1+L, thus t1=L/(c-v).

The blue and green are for the backwards trip.
The light path is blue, moving backwards, with a distance of c*t2.
The green is the clock, moving forwards, with a distance of v*t2.
We can see that now the length of the clock is equal to the light path blue the green line.
Thus L=c*t2+v*t2.

Or to express it differently, we see that the light path is the orange line minus the green line:
c*t2=L-v*t2.

Either way, you end up with t2=L/(c+v)


And there is nothing wrong with the times overlapping like that. Just consider a stationary clock, with the light bouncing back and forth, the times will always overlap.

In order to avoid that overlap, you would need to flip the entire system around at each reflection, effectively to present it from the perspective of the light.
This keeps the light always moving to the right, while the system switches between moving left and right at each reflection (and turns around so the light always moves from the left to the right).

Escape velocity of any inertial frame is always less than the velocity of light. So a pulse doesn’t have to obey the rules of inertial frame -Right?

Horizontal light clock does obey the postulate of “ Laws of physics are the same in all inertial frames" - Right?

Vertical light clock doesn’t obey the postulate of “ Velocity of light is constant in all inertial frames. Constant “c” means its direction is also constant in the direction in which a pulse is fired - Right?

Distance covered by a clock in one second = Red line - Blue line = vt = ct1-ct2
Velocity of clock = C(t1-t2)/t 
while in your case in upper diagram
Velocity of clock = C(t1+t2)/t
Similarly, would overlap affects length cntraction?  I mean would it be (ct1 -ct2) or still it is ct1+ct2

No, it starts going forward from the back mirror. It strikes the front mirror, bounces, and starts going backwards.

The fact that your first diagram has it moving forwards should be a good indicator that you are doing something wrong.

My diagram is corrected one. Your version is in the following link. https://worldscienceu.com/lessons/18-4-length-contraction-examples-horizontal-light-clock-copy/

Escape velocity of any inertial frame is always less than the velocity of light.

Escape velocity has no meaning there. That applies to a body in a gravitational field or the like.

Horizontal light clock does obey the postulate of “ Laws of physics are the same in all inertial frames" - Right?

Vertical light clock doesn’t obey the postulate of “ Velocity of light is constant in all inertial frames.

As long as both are inertial, then both require the laws of physics, including the speed of light, are the same as any other inertial frame.

Constant “c” means its direction is also constant in the direction in which a pulse is fired - Right?

No. It simply means the speed of light, in whatever direction it is propagating in, will be c.

Distance covered by a clock in one second = Red line - Blue line = vt = ct1-ct2

There are a few equivalent ways to do it. One is simply v*(t1+t2).
The other is purple plus green, which gives the same v*(t1+t2). (and that can also be orange plus purple minus orange plus green, the 2 orange cancel).

Of course, if we want to find the velocity, we divide by the total time, t1+t2.
Logically both of the above give us v, as we would expect.

And we can use the light paths, like you did. i.e. v=c*t1-c*t2 = c*(t1-t2)/(t1+t2), but why leave it at that. We already have expressions for t1 and t2.
This simply becomes:
c*(t1-t2) = c*[L/(c-v) - L/(c+v)]
=c*L*((c+v)-(c-v))/(c^2-v^2)
=c*L*2*v/(c^2-v^2)
=2*L*c*v/(c^2-v^2)

And t1+t2, as provided above (i.e. in prior post) is:
(t1+t2)=2*L*c/(c^2-v^2)

So c*(t1-t2)/(t1+t2) = [2*L*c*v/(c^2-v^2)]/[2*L*c/(c^2-v^2)]
=v

Just like we would expect.

Now lets try the other option, this incorrect one you bring up:
v=c*(t1+t2)/(t1+t2).
v=c

Notice the problem?
We end up with the clock travelling at the speed of light.
If that was the case, ignoring the physical impossibility) the light would never leave the back of the clock on its trip to the front.
We can even see the effect of that on the equations for t1 and t2.
t1=L/(c-v)=L/(c-c)=L/0.
You can't divide by 0.
t2 isn't as much of a problem, it would simply be t2=L/2c
But the total time still is a problem:
tt=2*L*c/(c^2-v^2)=2*L*c/(c^2-c^2)=2*L*c/0
Again dividing by 0.

So it is quite clear that makes no sense for multiple reasons and cannot be correct.

My diagram is corrected one. Your version is in the following link. https://worldscienceu.com/lessons/18-4-length-contraction-examples-horizontal-light-clock-copy/

No, your diagram is wrong, as is that video.
As it is a video it also provides a second way to tell. Look at just how much slower the light is travelling in the second part.
Remember, the speed of light has to be constant. There is no way to have it continue to move forward after the reflection as it would either just hit the side again, or need to slow down.
He likely did it that way so it would all fit up the top, rather than making it correct.
Also notice how he provides no justification for where he gets the distance from.
Sure, it still needs to be c*t2, but it doesn't need to be =L-v*t2.

Here is a diagram, just focusing on that trip:


Just like the prior one, the blue line is the the path light has allegedly taken. This has a length of c*t2.
The green line is the distance the clock has moved. This has a length of v*t2.
The orange line is the length of the clock. This has a length of L.
From this image we can clearly see green=blue+orange.
This means instead of the equation I clearly derived and the one he provided with no justification, you end up with this:
v*t2=c*t2+L.
To solve this for t2, you follow a similar procedure to before:
v*t2-c*t2=L
t2*(v-c)=L
t2=L/(v-c).
And there we have a big problem. Unless v is greater than c (which is impossible) the time is negative.

So now, instead of solving for t2, lets solve for v.
v=c+L/t2
This shows that we need to have v faster than the speed of light to have this happen.

This is also understandable from the diagram, and video.
As both the light pulse and the clock are moving to the right, the only way for the clock to "overtake" such that the light appears to move from the front to the back is if the clock moves faster than light.

Or to instead go from reality, as the light is moving forwards from the front of the clock, it will continue to get further and further ahead, never reaching the back of the clock.

So it doesn't matter how it is dressed up, that video and that diagram is simply wrong.
Upon reflection, the light must start travelling backwards (to the left), not simply slow down.
This means it must hit the left (or back) side of the clock before the clock travels its length, i.e. before the left side crosses where the right side was when the reflection occurred.

But also note, that that wasn't the equation that was provided in the video.
They did not have v*t2=c*t2+L.
Instead they provided the correct equation, the same one I had, c*t2=L-v*t2.

They provided the correct equations, but with an incorrect diagram, likely to make it look nicer and keep it all on the board.

To expand, rather than a simple diagram like that, here is a time-displacement graph showing the problem:

Or alternatively, interactively here:
https://www.desmos.com/calculator/effmq1spkt

The x axis is time.
The y axis is position.
The 2 solid black diagonal lines are the clock, moving along through at some velocity.
The red lines are the light moving forwards.
The blue lines are the light moving backwards.
The red dashed line is a continuation of the light moving forwards after hitting the front of the clock.
The purple dashed line is the time in the taken for a complete trip in the reference frame of the clock.
The orange line is that same time but viewed from the reference frame in which the clock is moving. The difference between these times is the time dilation.

Notice that the light bounces off the mirror and changes direction, switching between moving forwards and backwards.
Notice that the light path continuing from the clock doesn't hit it ever again.
Notice that the time taken to complete a cycle is different in the reference frame of the clock and the outside observer.

Here is what it looks like for a stationary clock, i.e. in the reference frame of the clock:

The orange line appears to be missing, but it is overlapping the purple line.
And here it is in a much more extreme example (90% of the speed of light):

With this setup, it takes longer for the light to go to the front of the clock than it takes for the entire cycle in the clock's reference frame.

Does this make it easier to understand?
Feel free to use the link and play with the variables.

If you want to remove the length contraction to see what affect that has change the 4th equation to be L=L_0

The upper diagram in the following picture is the diagram shown in the video.

I drew the lower diagram (the right one) when I caught the mistake in the video.

No, your diagram is wrong, as is that video.

So how come my diagram (lower diagram in the following picture)  is incorrect?


or



Regarding postulates:
A pulse is fired vertically in a vertical light clock but doesn't move in the original direction in which was fired but moves vertically/diagonally along frames. It's just because "laws of physics are the same in all inertial frames". Here velocity of the frame is added to '"c" but the same "c" is not subtracted from the velocity of light in the horizontal light clock.

- source Wikipedia

t=2L/c, base of triangle AA =vt'

The base of the time dilation triangle is AA=s=vt’ where t’ is dilated time.

The velocity of the moving frame relative to the stationary frame is v in time t where t is not dilated. Assume both mirrors of the light clock are permanently attached to the ceiling and floor respectively inside of the moving frame. This means mirrors also move at v in time t (where t is not dilated) relative to the stationary observer.

The spatial distance covered by the moving frame at any time t is s=vt (where t is not dilated) relative to the stationary observer. This means

The spatial distance covered by mirrors of the moving frame is also s=vt (where t is not dilated) relative to the stationary observer.

Since the aforementioned distances (s=vt’ and s=vt) are not equal therefore what would be the real position of mirrors or any stationary object inside the moving frame relative to the stationary observer.


Right angle triangle or closed triangle doesn't even form if dilated time t' is taken.

The aforementioned dilated time t' or s= vt' may be calculated from a horizontal light clock.

The upper diagram in the following picture is the diagram shown in the video.
I drew the lower diagram (the right one) when I caught the mistake in the video.
So how come my diagram (lower diagram in the following picture)  is incorrect?

I misunderstood/misexplained.
The top diagram is incorrect, the lower diagram in that picture is correct.

Regarding postulates:
A pulse is fired vertically in a vertical light clock but doesn't move in the original direction in which was fired but moves vertically/diagonally along frames. It's just because "laws of physics are the same in all inertial frames". Here velocity of the frame is added to '"c" but the same "c" is not subtracted from the velocity of light in the horizontal light clock.

By changing reference frames you change directionality. But you don't change the speed of light.

In the moving frame, the light travels at c bouncing back and forth between the mirrors, with only this vertical component.
In the stationary frame, which the clock moves in, there is a horizontal and vertical component to the speed of light.
The horizontal component is the same as the moving clock. And the vertical component has also changed.

Also note that when adding velocities which are so high, you can't use simple Newtonian relativity where u'=u'+v.
Instead you need to use the correct relativistic formula:
u=(u'+v)/(1+v*u'/c^2).
Now if u'=c, you end up with:
u=(c+v)/(1+v*c/c^2)
u=(c+v)/(1+v/c)
u=c*(c+v)/(c+v)
u=c.

But that is just colinear motion.
If the motion is perpendicular it is more complex.
Then you have:
u_y=sqrt(1-v^2/c^2)*u'_y/(1+v*u'_x/c^2)

Where u_x is the velocity of the object in the x direction and u_y is the velocity of the object in the y direction, with the ' versions being those to the stationary observer and the unprimed versions being relative to the observer in the moving reference frame.

If you do the proper relativistic additions it all works out, for both. The horizontal clock is above, but for the vertical one:
u'_x=0, and u'_y=c
So:
u_x=(0+v)/(1+0*v/c^2)
u_x=v

u_y=sqrt(1-v^2/c^2)*c/(1+v*0/c^2)
u_y=sqrt(1-v^2/c^2)*c
u_y=sqrt(c^2-v^2)

Now to find the total velocity we need to use vector addition. Fortunately, these are at right angles so we can use Pythagoras, i.a. a^2+b^2=c^2.
so u^2=v^2+(sqrt(c^2-v^2))^2
u^2=v^2+c^2-v^2
u^2=c^2
u=c

And thus we end up with it travelling at the speed of light in both frames, even though we add the velocity of the frame both times.
The main important part required is that it is added using the relativistic velocity addition formulae, rather than the Newtonian limit for low velocities.

The base of the time dilation triangle is AA=s=vt’ where t’ is dilated time.
The velocity of the moving frame relative to the stationary frame is v in time t where t is not dilated.

Be careful with using dilated time vs non-dilated time. It isn't a on or off thing, it is relative.
Time is dilated for both observers.

In instances like this, time t refers to the time in the inertial reference frame in which the clock is at rest, i.e. the left diagram.
Time t' refers to time in some other reference frame that the clock is moving in.
This convention is then applied to other aspects as well. e.g. above u is measured in the inertial reference frame with the clock at rest. u' is measured in the reference frame in which the clock is moving.

And you can make it more complex and confusing by noting that timing and order of events is also relative to the frame by instead of just having 1 moving clock, have 2 "identical" clocks, one in each reference frame.
Then both frames see the other frame as ticking more slowly than them, because each frame sees the other moving away.

The velocity of the clock in the frame using t is 0, and thus the base of the triangle is s=0.
The velocity of the clock, and the frame containing it, in the frame using t' is v, and thus the base is s'=v*t'.

There is no triangle which has a based of vt. There is no s=vt.

Right angle triangle doesn't even form if dilated time t' is taken.

Why not?
If anything it would be the other way around, where the setup without time dilation would be impossible as it would require light to travel faster than the speed of light.

I deduced time dilation to be = t’ = t(1+v^2/c^2)^0.5 when the base of the right-angled triangle is vt/2 instead of vt’/2 where t’ is the dilated time. Light clock moves with v in time t relative to outside observer therefore the base of the whole time dilation triangle is vt. not vt'

Since t’ is longer than t therefore outside observer unable to see what the inside observer sees in his time frame just like the sighting of a pulse in a horizontal light clock therefore a returning pulse should strike the lower mirror after the completion of one second in time t due to time dilation.

Similarly, Pls ref to the diagram. - Source Wikipedia
It states "Event B is simultaneous with A in the green reference frame, but it occurred before in the blue frame, and will occur later in the red frame"

The grey area is the light cone of the observer. Just wondering ct is perpendicular to the x-axis but x’ and x” are not perpendicular to the ct’ and ct” respectively. Since there are 3 time-axis (ct,ct’,ct”) and 3 space-axis (x,x’,x”) therefore shouldn’t be there 3 light cones

The tilting/rotation or squeezing of the space-time diagram depends upon the speed of observer relative to the observer who thinks s/he is at rest.
There are 3 time-axis (ct,ct’,ct”), 3 space-axis (x,x’,x”) and hence 3- light cones.

Construct the 3-light cones such that 2 of the light cones are tilted relative to the observer who is at rest. Let
A is surface of the base of a light cone of x-ct
B is surface of the base of a light cone of x’-ct’
C is surface of the base of a light cone of x”-ct”
At Apex (common point)
All observers would be able to see each other when they are at rest
Beyond Apex
Relative to the observer on A, observers on B and C are either above or below A.
Above is for future while below is for past. Since observer on A can’t see things either in future or past, therefore, none of the observers would be able to see each other as soon as 2 of the observers starts moving with different velocities due to tilting of the surface of basses of light-cones. In a nutshell, observers can’t see each other if their speed is not the same – is it possible?

I deduced time dilation to be = t’ = t(1+v^2/c^2)^0.5 when the base of the right-angled triangle is vt/2 instead of vt’/2 where t’ is the dilated time. Light clock moves with v in time t relative to outside observer therefore the base of the whole time dilation triangle is vt. not vt'

For what we have been doing, time dilation is t'=t/sqrt(1-v^2/c^2).
This would mean that t=t'*sqrt(1-v^2/c^2).

Again, there is no triangle where s=vt/2.
t is measured inside the frame moving with the clock.
In this frame, v makes no sense as it is measuring the velocity of this frame.
There is no right angle triangle in this frame. It is just going back and forth.

The frame with t' is the one with the clock moving. This is the frame where v makes sense.
You need this frame to be able to get the triangle.

You only ever get s=vt'/2. You never get s=vt.

Since t’ is longer than t therefore outside observer unable to see what the inside observer sees in his time frame just like the sighting of a pulse in a horizontal light clock therefore a returning pulse should strike the lower mirror after the completion of one second in time t due to time dilation.

Mostly right.
The outside observer sees the same events take longer.
If it takes 1 second inside the moving frame for the light to appear to bounce back and forth, then for the outside observer which sees the clock as moving, it will take more than 1 second to complete the bouncing backing and forth.

The grey area is the light cone of the observer. Just wondering ct is perpendicular to the x-axis but x’ and x” are not perpendicular to the ct’ and ct” respectively. Since there are 3 time-axis (ct,ct’,ct”) and 3 space-axis (x,x’,x”) therefore shouldn’t be there 3 light cones

In this case, there should only be 1 light cone.
This is because the light cone is for the observer at the centre.
Different velocities will change the frequency of light and some other things, but it will not change the regions that are in your light cone.
Changing your velocity will not allow you to see things you can't as they are out of your light cone.

You would get multiple light cones if you have multiple observers in different positions.

As for the axes, you wouldn't expect them to be perpendicular for all frames in this diagram.
If you convert the diagram to different frames then whichever frame you choose will be perpendicular, but other ones will not.

The speed of light is constant. That means if you draw a line from the observer at 45 degrees, it follows the speed of light and that is the same regardless of reference frame.
This causes the "horizontal" and "vertical" lines to cross along this 45 degree line, and that applies for all the reference frames.
That makes it impossible to simply rotate the frame and instead you need to skew it as well.

The other aspect is simultaneity and how it varies, which this skewing covers.

“t” is measured inside the frame moving with the clock.
In this frame, v makes no sense as it is measuring the velocity of this frame.

True but this is the same “t” in which a light clock moves with “v” in the right direction relative to an outside stationary observer whose clock was synchronized with the same light clock when it was stationary – Right?

Therefore distance covered by mirror(s) relative to stationary observer is = s=vt

If the base of the triangle is vt’ then it also means t’=t.

Mirrors move in t not in t’ relative to a stationary observer.

No idea if “c” can have components. Doesn’t a pulse go under stress if it has unequal horizontal and vertical speed/velocities components?

Similarly, there is no gravitational field underneath a moving light clock therefore what changes the components of the speed of a pulse or anything else (e.g. if a ball drops or it up and down motion)?

Even if it has a horizontal component then what path of a pulse (option 1 or option 2) would you choose for the light clock as shown below?

Quote

“t” is measured inside the frame moving with the clock.
In this frame, v makes no sense as it is measuring the velocity of this frame.

True but this is the same “t” in which a light clock moves with “v” in the right direction relative to an outside stationary observer whose clock was synchronized with the same light clock when it was stationary – Right?

No, it isn't.
That is the point I am making.
The time t is only for the frame in which the clock is stationary. The clock is not moving in this frame.
The frame with the clock moving has t', not t.

Synchronising the clocks before motion doesn't help. This is because as soon as you accelerate the clock, that synchronisation is lost.
Due to time dilation, the clock will then appear to tick slower for the outside observer as it is now travelling at some velocity relative to it.
All that would do is introduce a third time, which while equal to t, doesn't describe the same thing.
That would be the purple dashed line in the graphs I presented. While the clock is stationary it matches the time taken. But when the clock is moving, for the outside observer that is just a portion of the cycle time.
Thus it is not the time taken for the light to bounce between the 2 mirrors.

So no, the only distance there is to calculate is s=v t'
The distance covered by the mirrors relative to the stationary observer, in the time it takes for the moving clock to complete a full cycle is s=v t'.
It is NOT v t. The only time it will ever be s=v t is when the clock is stationary and thus v=0 so s=0.

No idea if “c” can have components. Doesn’t a pulse go under stress if it has unequal horizontal and vertical speed/velocities components?

That would require preferred directionality for the universe and would mean light could only ever propagate along those preferred directions.

All these components mean is that it is going in a particular direction. And you can happily rotate your reference.
For example, consider light propagating directly along the x axis. That has an x component of c and a y and z component of 0.
But you can rotate your reference, such that that X axis is along any direction, for example, at 30 degrees to the original x axis. Then the light will have a X component of c*cos(30deg) and a Y component of c*sin(30deg).

So there is nothing at all wrong with light having velocity components in orthogonal directions. All it means is that it isn't travelling aligned to the axes.
And there is no need for them to be equal, and not being equal would not induce stress.

Stress would only be induced by the velocity varying across the object. But as a photon is a point particle, that can't happen.

Similarly, there is no gravitational field underneath a moving light clock therefore what changes the components of the speed of a pulse or anything else (e.g. if a ball drops or it up and down motion)?

The only thing changing the speed is the mirrors causing it to reflect.
Otherwise it is just picking a different reference to measure the speed.

Even if it has a horizontal component then what path of a pulse (option 1 or option 2) would you choose for the light clock as shown below?

Option 2 is the closest.
Figure 1 and Figure 2 are fundamentally incorrect as it has the light teleporting.
The light path needs to be continuous, with the arrows indicating the direction continuing to point along the path of the light.

However, if we ignore that directionality, you will have either option 1 or option 2 depending on the speed.
For low speeds you will have something similar to option 2, for high speeds you will have something similar to option 1.
This is not a contradiction as the light isn't just moving horizontally, and the vertical speed allows it to continue moving forwards but down.
There is also a case where it actually bounces straight down and up. This is the crossover point between the previous 2 cases. This occurs when v=c*Lh'/Lv, where Lh' has had the relativistic contraction applied, i.e. Lh'=Lh*sqrt(1-v^2/c^2)
This means it occurs when v=c*Lh/sqrt(Lh^2+Lv^2), or v=c*Lh/Ld, where d is the diagonal length.
For a square rotated 45 degrees, this amounts to ~70% the speed of light. (c/sqrt(2))

There is also the issue of just how "no time dilation" would work.

The best case would be no special relativity and having the speed of light vary.
In which case it would be like having the system translate along.

Here are some GIFs for you, I'll just have a simple system which is a square rotated 45 degrees (note, the light travels at a constant speed in each gif, but differently between the gifs):
First, the stationary clock:

Now, a low speed one (50% the speed of light):

We notice that this matches option 2. But we can also hopefully realise that this needs to be on a spectrum between the stationary clock and some other end point.
So if we keep increasing the speed, the triangle at the bottom will shrink.
Here is the ~70% of the speed of light:

We see that this has hit the sweet spot where light just goes down and up for the bottom part of the trip.
And logically we can keep going.
This is 90% of the speed of light:

We see that now the light doesn't travel to the left at all.
But there is still no violation of any physical laws, as the light is merely changing direction.

But I can also make some for the cases where we completely ignore relativity.
If we do, and allow the speed of light to vary and ignore length contraction, we end up with this for a system travelling at 50% of the speed of light:

Here we notice light massively change speeds to go to the bottom section.
And here it is for 90%:

Again, a massive change in speed, more so than last time.

Doesn’t a light clock move relative to the outside stationary observer and in his time frame “t”. This observer measures the velocity of the light clock in time t, not in dilated time t'. Anyway

However, if we ignore that directionality?

I don’t understand?

Option 2 is correct in all cases. Don’t be confused like a professor in the aforesaid video. I have not yet done the calculation but I believe a pulse goes out of course in its a round trip. Here C-V is applied.

At high speed: Max distance a mirror A can cover in its round trip is less than AC before a pulse hits A. The combined length/distance of CD and DA is much greater than the distance covered by mirror A in a round trip (<AC ). We can play with the design of the light clock by just changing its angle theta. 


Round Trip: A pulse traces out a path at 45 degrees (original angle ACD) if a pulse doesn't have a horizontal speed component - so it misses its target D and A as well.

Doesn’t a light clock move relative to the outside stationary observer and in his time frame “t”. This observer measures the velocity of the light clock in time t, not in dilated time t'. Anyway

No. That is what I have been repeatedly trying to explain.
t is the time in the reference frame.
That is the time measured for a clock cycle in that reference frame.

t' is that same time but as observed by an observer who sees the reference frame and clock moving.

That is why in that diagram you have the length being specified as s=vt'.

Quote

However, if we ignore that directionality?

I don’t understand?

The directionality of the light along the path you have drawn.

As you have drawn it in Figure 1, you have light starting at the left side, moving up, reflecting and moving back down to hit the middle.
You then have more arrows showing it does from the right side downwards, reflecting off the bottom and then meeting in the middle.
It is the directionality of the light along this path I was talking about.

With this directionality, it is impossible as the light is teleporting.

However, if we ignore it and have it start on the left and just go to the right, then it is possible.

Option 2 is correct in all cases.

No it isn't.
I provided 2 examples, done with the correct relativistic calculations, where it is not.

And there are other justifications as well.

Your diagram allows the diamond to be squashed, giving us 2 extremes:
If theta1=0 and theta2=90 degrees, then this is the horizontal light cock, and will behave exactly like that.

If theta2=0 and theta1=90, then this is the vertical light clock and will behave exactly like that. This is inconsistent with option 2.
In fact, it is more consistent with figure 1, as with the length of the horizontal component being 0 there will be no asymmetry between the top and bottom. And as it needs to be on a sliding scale between them, there must be a case where it is like figure 2 as well.

And as shown above (in the figures I provided), when you take length contraction into it, you can even get it with a square. Without length contraction, this will only happen if v is equal to the speed of light for a square.

At high speed: Max distance a mirror A can cover in its round trip

Don't just focus on the round trip.
Focus on the trip from C to D to A.
Consider the following possibility.
The light, after reflecting of mirror C travels straight down, with only a vertical component to its velocity. It then reflects off mirror D and travels straight up to reach mirror A.
This is because during this time, mirror A has moved from its location, to the location where mirror C was.

Letting the distance from B to D = Lv, the light has travelled a distance of 2*(1/2)*Lv = Lv, and thus the time taken can be found by noting that c*t' = Lv.
Thus t'=Lv/c

Letting the distance from A to C = Lh', the mirror has travelled a distance of Lh', and thus v*t'=Lh
This means that v=Lh'/t' = Lh'/(Lv/c)=c*Lh'/Lv.

That means if we have a velocity of c*Lh'/Lv, we will get the light to bounce straight down and up.
Or to express it without fractions, we need:
v*Lv = c*Lh'

But before just jumping straight into that, we need to note that Lh is not the same as Lh'.
Lh is the clock frame, Lh' is the frame the outside observer is viewing it in.
Lh'=Lh*sqrt(1-v^2/c^2)

Thus we need:
v*Lv = c*Lh*sqrt(1-v^2/c^2)

By squaring both sides we get:
v^2*Lv^2 = c^2*Lh^2*(1-v^2/c^2)
v^2*Lv^2 = c^2*Lh^2-c^2*Lh^2*v^2/c^2
v^2*Lv^2 = c^2*Lh^2-Lh^2*v^2
v^2*Lv^2 + Lh^2*v^2 = c^2*Lh^2
v^2*(Lv^2 + Lh^2) = c^2*Lh^2

Then taking the square root of both sides we get:
v*sqrt(Lv^2 + Lh^2) = c*Lh

i.e. we need v=c*Lh / sqrt(Lv^2 + Lh^2)

That is easily achievable and thus option 2 is not always correct.

No. That is what I have been repeatedly trying to explain.
t is the time in the reference frame.
That is the time measured for a clock cycle in that reference frame.

t' is that same time but as observed by an observer who sees the reference frame and clock moving.

That is why in that diagram you have the length being specified as s=vt'.

You are right but what I'm trying to say that clocks of both the inside and outside observers are synchronized (tik tok at the same rate "t") at rest before the journey of the light clock into deep space relative to the outside observer who is stationary. So a vertical clock moves in time "t" relative to an outside observer. This makes the whole base of the triangle "vt". This means the half base of the right-angled triangle = vt/2. So how come vt'/2 = vt/2 when t' is longer than t.

Similarly, let t is time takes a pulse from A to B and B to C relative to an outside observer. A pulse strikes C simultaneously for both inside and outside observer but in their respective time frames. An outside observer must wait the same amount of time “t” so that a pulse completes its round trip for (relative to) the inside observer.  This means a pulse strikes A for outside observer earlier than for inside observer even if it (a pulse) doesn't out path. So a pulse doesn’t strike A simultaneously for both observers but differently. How would one observer know that a pulse has completed its path (one full second) relative to the other observer's time frame?

A pulse out of the path in its round trip: Since we can’t deduct the horizontal component of the speed of “c” that is equal to the velocity of the light clock, therefore, a pulse takes its initial direction (at an initial angle of 45 degrees) in which it was bounced from C no matter what the velocity of the light clock is.

See how things change quickly in the light clock of Einstein's version but with a slight change. Let theta =120 degrees.

You are right but what I'm trying to say that clocks of both the inside and outside observers are synchronized (tik tok at the same rate "t") at rest before the journey of the light clock into deep space relative to the outside observer who is stationary. So a vertical clock moves in time "t" relative to an outside observer. This makes the whole base of the triangle "vt". This means the half base of the right-angled triangle = vt/2. So how come vt'/2 = vt/2 when t' is longer than t.

Because of time dilation. Once more, vt is not vt'.

If you synchronise the clocks and then accelerate one of them to a constant speed of v, then time will appear to slow down. The clock that is observed to be moving will appear to tick more slowly than the clock that is observed to be stationary.
That is the whole basis of time dilation.

To explain more simply, you have 2 observers, Alice and Bob.
They have 2 identical clocks.
This means for each of them, they see their clock complete in a time of t.
Bob only cares about his clock and is the one moving at a velocity of v relative to Alice (with his clock).

Alice, watching both clocks sees a pulse start in both clocks simultaneously.
After time t, she sees that her clock has had the pulse complete, but Bob's clock is still going.
Only after time t', which is greater than t, she sees that Bob's clock has finished its pulse.


This means the base of the triangle is vt', not vt.

Similarly, let t is time takes a pulse from A to B and B to C relative to an outside observer. A pulse strikes C simultaneously for both inside and outside observer but in their respective time frames. An outside observer must wait the same amount of time “t” so that a pulse completes its round trip for (relative to) the inside observer.  This means a pulse strikes A for outside observer earlier than for inside observer even if it (a pulse) doesn't out path. So a pulse doesn’t strike A simultaneously for both observers but differently. How would one observer know that a pulse has completed its path (one full second) relative to the other observer's time frame?

That is another key part of relativity. Events are not simultaneous in all reference frames. This also causes some apparent paradoxes.
For the outside observer, they would see the pulse take longer to travel A->B->C than it takes to travel C->B->A. And the inside observer sees both paths take the same amount of time, which is in between the 2.

This means if you set the time it strikes C to be 0, then it will leave A earlier in the stationary frame, and arrive at A earlier, but take longer for the round trip.
You can do the math based upon the velocity to determine when it will be complete in each reference frame.

A pulse out of the path in its round trip: Since we can’t deduct the horizontal component of the speed of “c” that is equal to the velocity of the light clock, therefore, a pulse takes its initial direction (at an initial angle of 45 degrees) in which it was bounced from C no matter what the velocity of the light clock is.

You can't just take the velocity and add it as in Newtonian relativity.
You need to do the proper relativistic velocity addition.
This also makes the reflection more complex.

For example, in the animations I provided, when stationary, the reflection at C was normal.

But as the velocity increased, it became less normal, until at a very high velocity, it appeared to just defect it slightly instead of a normal reflection.

That is another key part of relativity. Events are not simultaneous in all reference frames. This also causes some apparent paradoxes.

You are mixing things.

A pulse strikes at the lower or upper mirror simultaneously for both observers in the vertical clock but in their respective time frames.

Such striking of a pulse at A, B, C, and D in diamond shape light clock are not simultaneous for both observers.

You have to be consistent.

Regarding relativity simultaneity:

Fig#1: Let a remotely controlled spaceship is moving close to the speed of light [say 0.9c] relative to a stationary observer on an asteroid. Onboard observer sends a signal (pulse) with the help of a remote control device from the back of the ship to its front.

For onboard observer: A pulse has already arrived at the front and a spaceship has stopped just in front of the explosive.

For asteroid’s observer: A spaceship is destroyed due to an accident (explosion) as a signal (pulse) has yet to arrive at the front to stop the spaceship.

So who is right in reality when the spaceship is stopped?

Fig 2: A stationary observer has a binocular that adjusts itself automatically with the speed of the moving vertical clock such that he sees his clock is synchronized with the moving vertical clock at all times. No time dilation is observed here – why?

Fig-3: Let a train moves towards a stationary observer. Which observer would be found killed A or B by the thunder of light that struck the longitudinal sides of the train at the same time relative to the stationary observer when a train stopped?

For the outside observer, they would see the pulse take longer to travel A->B->C than it takes to travel C->B->A. And the inside observer sees both paths take the same amount of time, which is in between the 2.

So does this mean dilation of the first half is balanced by the contraction of the second half? - No time dilation after the completion of one round of a pulse.

Such striking of a pulse at A, B, C, and D in diamond shape light clock are not simultaneous for both observers.

Do you mean it doesn't happen at the same time for both observers, or 2 events 1 observer sees is not simultaneous?

1 is time dilation, the other is the issue of simultaneousness.

The easiest way to see it is to have 2 counter-propagating pulses, both starting at B (or 2 running the same way, but one starting at B and the other at D)
First, we consider the observer moving with it.
They see them arrive at A and C simultaneously, and then see them reach D simultaneously, and then see them get back to A and C simultaneously and then see them reach B simultaneously. Each reflection is simultaneous.

But now for the outside observer, while both pulses leave B at the same time, they see the pulse moving backwards take much less time and thus arrive sooner at A than the pulse travelling towards C. Then, they see both arrive at D at the same time, and so on.

Regarding relativity simultaneity:

Fig#1: Let a remotely controlled spaceship is moving close to the speed of light [say 0.9c] relative to a stationary observer on an asteroid. Onboard observer sends a signal (pulse) with the help of a remote control device from the back of the ship to its front.

For onboard observer: A pulse has already arrived at the front and a spaceship has stopped just in front of the explosive.

For asteroid’s observer: A spaceship is destroyed due to an accident (explosive) as a signal (pulse) has not yet arrived at the front to stop the spaceship.

So who is right in reality when the spaceship is stopped?

This is what I meant when I said it gives rise to apparent paradoxes, which aren't really paradoxes.

This is made quite vague so it isn't clear what is happening when and relative to who.
It also relies upon instant acceleration which makes no sense as it raises the question of whose instant it happens in.
This is quite like a well known paradox with a train.

With this paradox, a train is moving at quite some speed and passes through a tunnel. If the train was at rest, it would be longer than the tunnel. Due to length contraction the train is shorter than the tunnel. Thus in the instant the tunnel is entirely within the tunnel, the doors of the tunnel close, and they reopen before the train leaves the tunnel.
The paradox alleges that in the frame of the train, in the instant the doors close, the train cannot fit inside the tunnel, especially as length contraction would make the tunnel shorter, and thus the train should be cut by the doors.
The problem is that the instant was for the outside observer, and with simultaneous events depending on reference frames, each door closing is not simultaneous for the observer in the train. Instead the observer in the train sees the door at the end of the tunnel close first and then the door at the entrance close after the train has already started leaving the tunnel.

In general, if an object is moving to the right, and 2 events occur simultaneously to an outside observer, the event on the right will appear to happen first to an observer moving with the object.
And likewise, if 2 events occur simultaneously for the moving observer, the event on the left will appear to occur first to the stationary observer.

It is the same kind of issue here. (as well as issues with length contraction)

You want to have the front of the rocket some distance from the explosive at the same time as someone triggers an event at the back of the rocket.
This can only be simultaneous in 1 reference frame. So you can pick it to occur in the reference frame of the rocket, or the reference frame of the observer.
In general, you want the distance the rocket needs to cover to be equal to the distance the light needs to travel in the rocket.
So first if it is the case of the onboard observer.
They see the distance is correct and press the button, sending the light and having it reach the front just in time.
To the outside observer, they event to the left occurs first, they see the button is pushed before the distance is reached, and that gives the light enough time to reach the front.

Conversely, with the setup where the outside observer sees it simultaneously, there isn't enough time for the light to reach the front and so it passes the point of the explosive before it reaches the front.
But the onboard observer now sees it reach that point, but doesn't push the button until later, and thus the signal is sent too late.

Fig 2: A stationary observer has a binocular that adjusts itself automatically with the speed of the moving vertical clock such that he sees his clock is synchronized with the moving vertical clock at all times. No time dilation is observed here – why?

This makes no sense.
How are these binoculars adjusting themselves to make the clock appear synchronised?
That can be summarised as saying A stationary observer has a magic device so no time dilation occurs. Why does no time dilation occur?
You need to explain how the device works to show that it is possible before saying there is a problem.

Fig-3: Let a train moves towards a stationary observer. Which observer would be found killed A or B by the thunder of light that struck the longitudinal sides of the train at the same time relative to the stationary observer when a train stopped?

If the lightning crossed in an instant, it would be the same in both frames as you are not looking at points in time along different positions along the direction of motion.
If it doesn't, then you are back to the light clock, with length contraction and the different angles making it hit the same one.

Quote

For the outside observer, they would see the pulse take longer to travel A->B->C than it takes to travel C->B->A. And the inside observer sees both paths take the same amount of time, which is in between the 2.

So does this mean dilation of the first half is balanced by the contraction of the second half? - No time dilation after the completion of one round of a pulse.

The time dilation is not balanced. The extra time required for the pulse to travel forwards is longer than the less time required to go backwards, and in cases where v is great enough, the forwards trip alone can take longer than the entire cycle in the stationary case. As the velocity approaches the speed of light, it approaches an infinite amount of time required. But the shortest time it can take for the backwards trip is 0.

You want to have the front of the rocket some distance from the explosive at the same time as someone triggers an event at the back of the rocket.
This can only be simultaneous in 1 reference frame. So you can pick it to occur in the reference frame of the rocket, or the reference frame of the observer.
In general, you want the distance the rocket needs to cover to be equal to the distance the light needs to travel in the rocket.
So first if it is the case of the onboard observer.
They see the distance is correct and press the button, sending the light and having it reach the front just in time.
To the outside observer, they event to the left occurs first, they see the button is pushed before the distance is reached, and that gives the light enough time to reach the front.

Conversely, with the setup where the outside observer sees it simultaneously, there isn't enough time for the light to reach the front and so it passes the point of the explosive before it reaches the front.
But the onboard observer now sees it reach that point but doesn't push the button until later, and thus the signal is sent too late.

I didn’t mention but the triggering button is fixed to the barrel from where a pulse is fired towards the front by the onboard observer. Similarly, chances of explosion relative to the outside observer are more when we increase the length of the spaceship. Triggering of the button at A is simultaneous for inside and outside observers. Spaceship stops at B’ just in front of the explosive.
Vertical clock and the path from A to B and from B to C in the diamond clock.
Outside observer sees the longer path of light but since outside observer also knows that inside observer in the moving frame feels stationary therefore whenever a pulse in the stationary light clock of stationary observer completes its path of 2L in time t, a pulse inside frame also completed its path of 2L in time t for an inside observer or vice versa. Here an outside observer compresses the time part of pulse for the inside observer despite knowing that a pulse has completed its path of 2L in time t when he talks about the longer path of light (the hypotenuse of the triangle). This last portion of the relativity of simultaneity is not mentioned.

This makes no sense.

Its not difficult to zoom moving object say a moving car via binocular. The auto adjustment of the zooming with speed of spaceship is just theoretical like the thought experiment.

The time dilation is not balanced. The extra time required for the pulse to travel forwards is longer than the less time required to go backwards, and in cases where v is great enough, the forwards trip alone can take longer than the entire cycle in the stationary case. As the velocity approaches the speed of light, it approaches an infinite amount of time required. But the shortest time it can take for the backwards trip is 0

Does time dilate at the same rate in all infinite types of the light clock if considered?

Triggering of the button at A is simultaneous for inside and outside observers. Spaceship stops at B’ just in front of the explosive.

Simultaneous doesn't make sense when you are comparing the time of a single event between 2 frames.
What you need to focus on is the multiple events in a given frame, or the time between them.

When is the button pushed?

Outside observer sees the longer path of light but since outside observer also knows that inside observer in the moving frame feels stationary therefore whenever a pulse in the stationary light clock of stationary observer completes its path of 2L in time t, a pulse inside frame also completed its path of 2L in time t for an inside observer or vice versa.

Is that time t both a measurement for an inside observer?
If so, then it is just saying that the inside observer sees the clock take time t and tells you nothing about how long the outside observer sees the clock take to tick.

If it is for both the outside and inside observer, again that is wrong and completely ignores time dilation. It ignores the fact that time is relative.

That would be like saying the inside observer sees the clock is stationary and thus the outside observer will measure it to be stationary as well. It is completely false.

Knowing that time dilation is occurring doesn't mean it stops occurring.

Its not difficult to zoom moving object say a moving car via binocular.

And all that zooming will do will keep the ship the same angular size. It won't affect the observed speed that the clock ticks at.

Does time dilate at the same rate in all infinite types of the light clock if considered?

Yes. As long as the clock is a rigid loop, i.e. it returns to its starting point in the frame it is stationary in and the parts of the clock do not move relative to each other other than the photon of light moving through it, then the time dilation will be the same, regardless of what path the light takes.

Simultaneous doesn't make sense when you are comparing the time of a single event between 2 frames.

I meant firing of the pulse is simultaneous for both observers just like
- Alice, watching both clocks sees a pulse start in both clocks simultaneously.
-she sees that Bob's clock has finished its pulse.

Similarly, when a pulse returned to its starting point in both vertical and horizontal light clocks

The base of the triangle made by the light path in the vertical light clock must equal to the distance covered by the horizontal light clock (purple + green) but they are not due to the reasons dilated time is used in the length of base vt’ while un-dilated time is used in the second one. Both t1 and t2 used in the horizontal light clock are undilated.

Sighting of both observers meet at the same one pulse in the vertical light clock but it doesn’t in horizontal version as well in all other types of light clocks where the similarity exists. 

The postulate of laws of physics are the same in all inertial frame is invalid when a pulse moves opposite to the direction of moving ship/clock in this trip of the pulse can’t be used for the derivation of time dilation equation and the same is applied to all infinite types of light clocks. Dilation and Compression can't be mixed.

It won't affect the observed speed that the clock ticks at.

Since the speed of zooming and the speed of the light clock are the same therefore an outside stationary observer sees a moving clock as stationary as his stationary light clock.

Quote

Simultaneous doesn't make sense when you are comparing the time of a single event between 2 frames.

I meant firing of the pulse is simultaneous for both observers just like
- Alice, watching both clocks sees a pulse start in both clocks simultaneously.
-she sees that Bob's clock has finished its pulse.

Then, for the outside observer, they see the pulse in their clock finish first, and then see the pulse in the moving clock finish second.

But for the moving observer, they see the pulse in their clock finish first, and see the pulse in the stationary clock finish second.

The base of the triangle made by the light path in the vertical light clock must equal to the distance covered by the horizontal light clock (purple + green) but they are not due to the reasons dilated time is used in the length of base vt’ while un-dilated time is used in the second one. Both t1 and t2 used in the horizontal light clock are undilated.

No, the 2 distances are the same.
Both distances are using the dilated time, where the clock moves vt'.
In my first derivation I used to instead of t' and ti instead of t.
t1 and t2 were both lengths of time for the observer who sees the clock move and thus would also be dilated time.

The postulate of laws of physics are the same in all inertial frame is invalid when a pulse moves opposite to the direction of moving ship/clock in this trip of the pulse can’t be used for the derivation of time dilation equation and the same is applied to all infinite types of light clocks. Dilation and Compression can't be mixed.

The only reason it appears to be invalid is because you are ignoring the relativity of order of events.

The fact that you cannot easily derive a formula for time dilation from this doesn't mean that it doesn't exist and that the laws of physics are invalid.

Quote

It won't affect the observed speed that the clock ticks at.

Since the speed of zooming and the speed of the light clock are the same therefore an outside stationary observer sees a moving clock as stationary as his stationary light clock.

No, it is still moving. It doesn't matter that it is being magnified to keep the same angular size, it is still moving and thus is still effected by time dilation.
Time dilation is based upon motion, not angular size.

Quote

Quote from: E E K on December 05, 2020, 10:08:36 PM
Quote
Simultaneous doesn't make sense when you are comparing the time of a single event between 2 frames.
I meant firing of the pulse is simultaneous for both observers just like
- Alice, watching both clocks sees a pulse start in both clocks simultaneously.

-she sees that Bob's clock has finished its pulse.
Then, for the outside observer, they see the pulse in their clock finish first, and then see the pulse in the moving clock finish second.

But for the moving observer, they see the pulse in their clock finish first, and see the pulse in the stationary clock finish second.

Let's try the other way. Pls ref to the following fig.

When a ship is stationary:

A light gun located in the middle of the ship fires two pulses as shown simultaneously (it means two events occur at the same point in space) when a button is pressed.

When a ship is stationary:

Both front and rear pulses completed a path of 2L simultaneously.
(c+c) = (c+c) = 2c = 2c or c = c

When a ship is moving:

Relative to an inside observer:
Both pulses completed a path of 2L simultaneously.
(c+c) = (c+c) = 2c = 2c or c = c

Relative to an outside observer:

A light path of both pulses is shown individually as well as combined.
Total path of the rear pulse = Total path of the front pulse
(c-v) + (c-v)  = (c+v) + (c-v)
(c-v+c-v) = ((c+v+c-v)
2c=2c or c=c

Both or either of the pulse can be used as a stopping signal in the aforementioned example.
A little more junks:

No, it is still moving. It doesn't matter that it is being magnified to keep the same angular size, it is still moving and thus is still effected by time dilation.
Time dilation is based upon motion, not angular size.

No doubt, the clock is moving in space but observer doesn’t see a longer path of light via auto- binocular. Its just like two frames moving with the same speed relative to each other.

Moreover, Alice, claims time dilate in Bob’s clock. Bob claims time dilate in Alice clock. The question is whose claim is right?  The answer is a light clock is not a clock anymore if moving. Here

Let Ch and Cv are the horizontal and vertical components of “C” (IMPOV impossible) respectively. Ch = Vh = speed of ship/clock. A light goes straight up or down with Cv only and goes forward straight horizontally with Ch=Vh only. Both Ch and Cv act together as “c” in a moving vertical clock and depend upon the initial angle that it makes with horizontal.

An outside observer sees mirrors of the vertical clock are moving away from a light at Vh = speed of ship in right direction therefore a light with Cv has to cover a longer in order to catch up the mirror as an outside observer sees mirrors of the vertical clock are moving away from a light.

Then, for the outside observer, they see the pulse in their clock finish first, and then see the pulse in the moving clock finish second.

But for the moving observer, they see the pulse in their clock finish first, and see the pulse in the stationary clock finish second.

A pulse covers an extra distance in moving clock by the time moving clock finfish second, but in the mean time a pulse in the stationary clock also covers an extra distance.

Total light path of the light in stationary clock is still equal to total path of light in moving clock.

Falling off any object from the ceiling of ISS is the best example wherein 90% of the earth's gravity acts on the said object. We can also imagine ISS close to the surface of the earth.

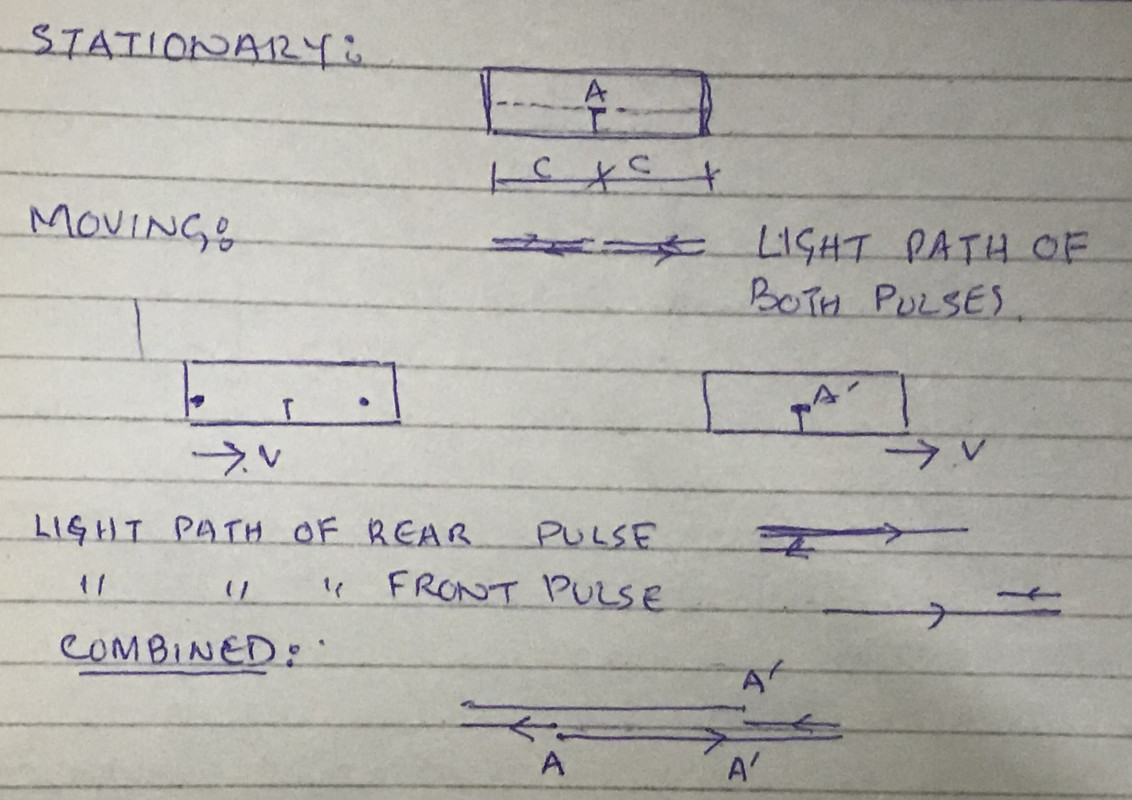
When a ship is stationary:

A light gun located in the middle of the ship fires two pulses as shown simultaneously (it means two events occur at the same point in space) when a button is pressed.

When a ship is stationary:

Both front and rear pulses completed a path of 2L simultaneously.
(c+c) = (c+c) = 2c = 2c or c = c

When a ship is moving:

Relative to an inside observer:
Both pulses completed a path of 2L simultaneously.
(c+c) = (c+c) = 2c = 2c or c = c

Relative to an outside observer:

A light path of both pulses is shown individually as well as combined.
Total path of the rear pulse = Total path of the front pulse
(c-v) + (c-v)  = (c+v) + (c-v)
(c-v+c-v) = ((c+v+c-v)
2c=2c or c=c

Both or either of the pulse can be used as a stopping signal in the aforementioned example.

And in this case, because the pulse starts and ends at the same point, them being simultaneous in one frame means they must be in every other frame. However the time taken can be different.

But note that the reflection is not simultaneous in all frames. Because this now happens at different points with those points separated in the direction of motion, they will only appear simultaneous to those with the same horizontal speed as the ship.
To those with a different horizontal speed (such as the outside observer at rest), they will occur at different times.
The outside observer at rest will see the reflection at the back occur first.

No doubt, the clock is moving in space but observer doesn’t see a longer path of light via auto- binocular.

Again, it doesn't matter what the observer sees.
The clock is still in motion, thus there is still time dilation.
Light travels based upon a linear velocity, not an angular velocity.

If you were watching 2 beams of light, one near and one far, the near one would have a higher angular velocity.
If you use different tools to view them to make them appear to have the same angular velocity, it wouldn't make the more distant beam actually travel faster or affect its motion in any way.

Likewise, viewing the moving clock through a different FOV will have no impact on the time dilation experienced.

Moreover, Alice, claims time dilate in Bob’s clock. Bob claims time dilate in Alice clock. The question is whose claim is right?

Both.
Once more, not only is time relative, but the order of events is relative, and that also makes time dilation relative.
No reference frame is preferred or absolute.
This goes back to this diagram you provided earlier:

Notice how the lines go?

Each of the lines which cross the time (e.g. ct) axis of the same colour corresponds to a period of time in that frame.
Every point along those lines is the same time in that frame.

I will focus on the red and blue, as they are the most extreme.
Consider a point along the red line at the second crossing after 0, this line is drawn as a thick red line with a thinner black line over the top.
The observer in the red frame will see it has taken 2 minutes to get to anywhere along this line. i.e. any event which occurs along this line will occur at time t'=2.
So lets consider 2 events along this line, marked with purple stars.
1 of these events occurs alone the blue ct'' axis, i.e. in the location where that observer is.
This will still take 2 units of time for red to see.
But for blue, it occurs at roughly 1.5 units of time.

So for red, they would correct in saying that it is taking them a longer period of time to observe events passing for blue and thus it appears to them that blue is going through time more slowly, but that is for events occurring where blue is.

The other event occurs along red's ct' axis. Now drawing a line for blue to see where it intersects their ct'' axis we see it takes ~2.8 units of time. i.e. that event took 2 units of time to reach for red, but 2.8 for blue.

So both observers see time dilated for the other observer.

This is because the 2 different locations are not simultaneous.
Red sees both events occur simultaneously, but blue sees one occur at time ct''=1.5 while the next occurs at time ct''=2.8, separated by roughly cdt''=1.3 time units.
(And to top it off, an event which occurred at time ct''=2, but along red's ct' axis, would occur at a time of ct'=1.5.

So both claims are right and both are based upon their own frame of reference and where the events are occurring.
This also means that you cannot accurately specify the timing of an event just by using time. You need time and location.

Let Ch and Cv are the horizontal and vertical components of “C” (IMPOV impossible) respectively.

Just what makes it impossible?

Consider any reference frame and consider a ray of light leaving from the origin.
If it travels along the x axis in the +x direction, then cx=c and cy=0.
If instead it travels along the y axis in the +y direction, then cx=0 and cy=c.
If instead it travels at some angle between then the cx and cy values will be between 0 and c, but will be such that cx^2+cy^2=c^2.

i.e. if it travels at an angle of a from the x axis, then cx=c*cos(a) and cy=c*sin(a).
Thus cx^2+cy^2=c^2*(cos(a)^2+sin(a)^2)=c^2.

All that saying the speed of light can be separated into its horizontal and vertical components is saying is that light can travel in any direction.

If instead you were bound to have cx=cy, you are saying that light can only travel away from the origin at an angle of 45 degrees.

Ch = Vh = speed of ship/clock. A light goes straight up or down with Cv only and goes forward straight horizontally with Ch=Vh only. Both Ch and Cv act together as “c” in a moving vertical clock and depend upon the initial angle that it makes with horizontal.

An outside observer sees mirrors of the vertical clock are moving away from a light at Vh = speed of ship in right direction therefore a light with Cv has to cover a longer in order to catch up the mirror as an outside observer sees mirrors of the vertical clock are moving away from a light.

In the reference frame of the clock vh=0.
The speed of light, cv is thus c.
To the outside observer, cv is not c.
It takes more time to cover the same vertical distance and thus cv is less than c.
This is because the light is now travelling at an angle and thus ch=vh, which is not 0.
This also means cv=sqrt(c^2-ch^2)=c*sqrt(1-ch^2/c^2)

A pulse covers an extra distance in moving clock by the time moving clock finfish second, but in the mean time a pulse in the stationary clock also covers an extra distance.
Total light path of the light in stationary clock is still equal to total path of light in moving clock.

No. That "the mean time" makes no sense as time is relative.
The observer moving with the clock will see it take some amount of time to complete.
The stationary observer sees it take longer and have a longer path length.

While it is the same physical path, the 2 observers see it take a different length due to the relative motion.

Ok how about the unit speed of light and speed ship/light clock?
Are they measured in meter/dilated second or just meter/second?
Let's go back to the right angle triangle used for the derivation of time dilation

Base = B= vt’/2
Perpendicular = P = L= ct/2
Hypogenous = D = Ct’/2

Let C and v are measured in meter/dilated second and c is in meter per second. Both C and c are not the same due to the difference in units.

D = [(0.5vt’)^2 + L^2]^0.5

Where D=Ct’/2, and L = ct/2

(Ct’/2)^2 = (vt’/2)^2 + (ct/2)^2

OR C^2 x t’^2 = v^2 x t’^2  + c^2 x t^2

OR t’^2 (C^2-v^2) =c^2 x t^2
OR t’ = t/ [(C^2-v^2)/c^2]^0.5 (edited) – Final Eq.

Here we can’t divide C or v by c due to the difference in units as explained above.

Similarly if c has to be measured in m/sec only then c and v can’t be multiplied with t’ as used in D=ct’/2 and base = vt’/2. In this case, the unit of vt’ or ct’ = (meter x dilated sec)/(sec) is not equal to the meter which is the unit of lenght as dilated second and second cant be canceled out.

Ok how about the unit speed of light and speed ship/light clock?
Are they measured in meter/dilated second or just meter/second?

Each person measures the speed of light for them in m/s.

The time dilation is only as you switch between the frames.
And that means that the speed of light can have different components in different frames.

The units are the same, they are just being measured in different frames.

If you wanted to try claiming they were different units, where 1 is measured in s and 1 is measured in s', then, taking the velocities to be c/s or c/s' or v/s' as appropriate, you don't end up with this as your final equation (also you left out the square root):

OR t’ = t/ [(C^2-v^2)/c^2] – Final Eq.

Instead you get this:
t'=t/[sqrt(c^2/s'^2 - v^2/s'^2)/(c^2/s^2)]
=t/[(s/s')*sqrt(1-(v/c)^2)]
=(s'/s)*t/sqrt(1-(v/c)^2)

Or:
t'*(1/s') = [t/sqrt(1-(v/c)^2)] * (1/s)

i.e. it is a conversion factor.

Just like if you have a length in mm and want to convert to inches you have l'=l*25.4 mm/inch
Your l in inches is multiplied by 25.4 mm and divided by inch to get the length in mm.

And so in this case, to convert from your undilated time t measured in s, you multiply it by a conversion factor which includes s'/s, to convert it to a dilated time t' measured in s'.

The equation of time dilation [t'=t/sqrt(1-v^2/c^2)] tells us how t’ and t are related to each other.

Conversion factor t/t’= sqrt(1-v^2/c^2)

There is no need to find the above said conversion factor in the t’ = t/ [(C^2-v^2)/c^2]^0.5.  if we know the conversion factor of  (s’/s) or how much is dilated second = second.

The equation of time dilation [t'=t/sqrt(1-v^2/c^2)] tells us how t’ and t are related to each other.

Conversion factor t/t’= sqrt(1-v^2/c^2)

There is no need to find the above said conversion factor in the t’ = t/ [(C^2-v^2)/c^2]^0.5.  if we know the conversion factor of  (s’/s) or how much is dilated second = second.

The point is that if you want to claim that t and t' aren't measuring the same units (seconds), as one is dilated, you need the units in the conversion factor as well.
The conversion factor includes this change of units.

e.g. the conversion factor for mm to inch isn't simply l/l' = 25.4
instead it is l/l' = 25.4 mm/inch.
That is because if you take the same physical length, then l is 25.4 mm while l'=1 inch.
That means that l/l' = 25.4 mm/inch.

So if you wish to assert that they are using different units then you need:
t/t’= sqrt(1-v^2/c^2) * (s/s')
That is because if you have some time t = a s, and some time t' = b s'.
That means t/t' = (a/b) * (s/s'), where a/b = sqrt(1-v^2/c^2).

So you need that change of units.

If however you accept that they are measured in the same units, then s/s' = 1, and it simplifies to:
t/t’= sqrt(1-v^2/c^2)

The speed of light is constant in all inertial frames so how would you measure the speed of light “c” or speed of any object in dilated time or in a frame where time slows down?

Frames within frame or spaces within space: Light clock when get compressed doesn’t even work if we play with the speed of the ships.

Spaceship A contains B
Spaceship B contains C
Spaceship C contains D
And so on

Spaceship A moves at a very high speed (say 0.8c) relative to outside stationary O

Spaceship B moves at a very high speed (0.6c) relative to outside stationary Oa 

Spaceship C moves at a very high speed (0.7c) relative to outside stationary Ob

And so on