Hope you may convince in my last try
NEWTON LAW OF GRAVITATION: The gravitational force
BETWEEN two masses = F GMm/d^
2 SPLIT ANALYSIS of Earth and Apple:
When an Earth is a gravitating mass and an Apple is a falling mass
Acceleration due to gravity of earth; g
e = GM/R^
2 (on the the surface of earth); where R = radius of earth.
So an apple fall on earth at the rate of g
eWhen an Apple is a gravitating mass and an Earth is a falling mass
Acceleration due to gravity of apple; g
a = Gm/r^
2 (on the surface of apple); where r = radius of apple
So an earth falls on an apple at the rate of g
aForce of Earth on Apple = Force of Apple on Earth
An apple falls due to g
e on Earth. The earth also moves upwards towards apple due to g
a of apple but by such a minuscule amount to be noticed or measured.
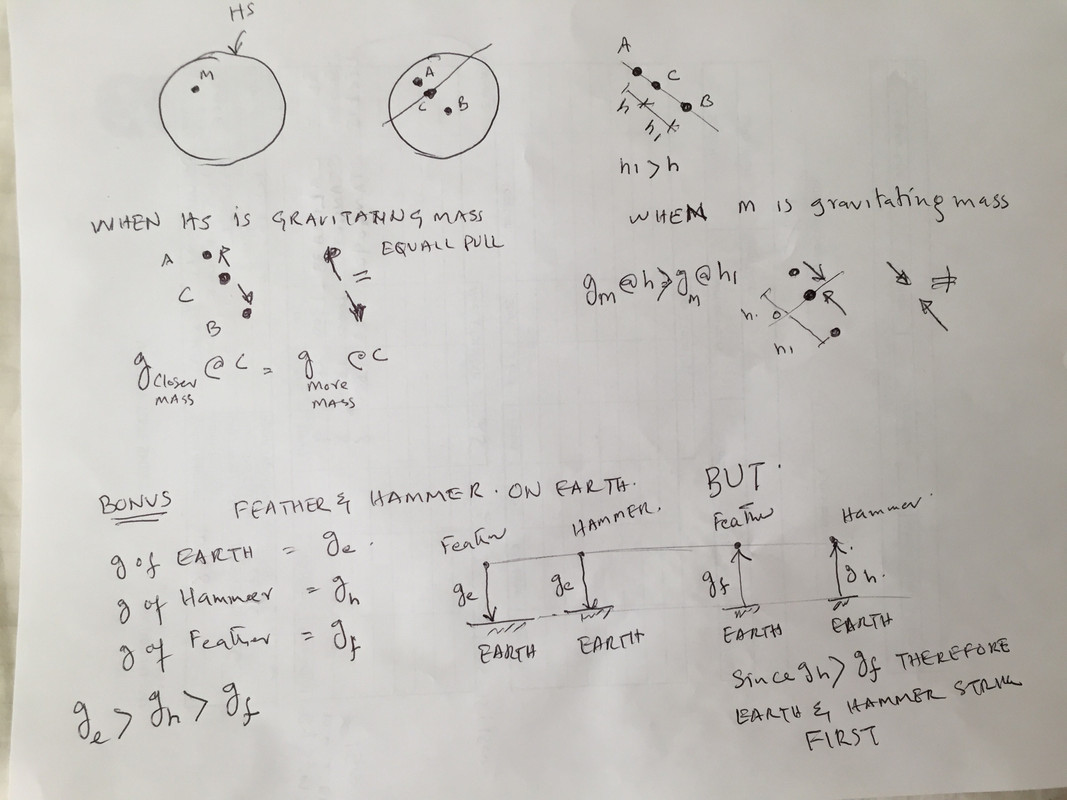
Shell Theorem
The presence of any mass M inside homogeneous Hallow Sphere HS. Two gravitational accelerations g are involved in this problem
1- Acceleration due to gravity g of HS
2- Acceleration due to gravity g of M
Three possible conditions
The g of HS < The g of M, The g of HS = The g of M, The g of HS > The g of M
Also, the size, mass, and shape of M can be varied and its location inside HS as well
According to shell theorem: The entire spherical shell exerts zero net force on M
This may be true as I said earlier but this is not the end of story. There is mammoth difference between
Gravitational Force
ON a mass and Gravitational Force
BETWEEN two masses
Newtons gravitational force is between two masses. Gravitational force on a mass is only considered during split analyses like Earth on apple and Apple on earth. Their combined effect appears in F = GMm/d^
2. As gravitational force is a force that attracts any objects with mass therefore HS attracts M but M also attracts HS.
The miscalculation in shell theorem is that HS attracts M but M doesnt attract HS.
SPLIT ANALYSIS of HS amd M
When HS is a gravitating mass and M is a falling mass
Mass on one side is closer, but there is more mass on another side.
There are three masses and three centers of gravities cg
A represents the cg of Closer mass
B represents the cg More mass
C represents the cg of M
The distance between A and C is h
The distance between B and C is h1
Obviously, h1 > h. The entire spherical shell exerts zero net force on M OK for the sake of arguments BUT the entire M also exerts a force on Closer mass as well as More mass of the HS. Here
When M is a gravitating mass and HS is a falling mass
Closer mass of HS falls on M with g of M
More mass of HS also falls on M with g of M
As h < h1 therefore the value of "g" of M at A > the value of "g" of M at B. Since net pull of M on two different parts of HS is not zero, therefore, Closer mass falls on M with little bit resistance from more mass of HS
Conclusion:
Accelerations due to gravities of Closer mass and More mass of HS may be cancelled at the center of M BUT the value of g of M at A is greater than the value of g of M at B due to the difference in heights therefore movement happens because of unbalance pull of M on two parts of the HS